들어가기 이전에 다음 글이 해당 자료구조에 대해 영어로 잘 설명해 놓았다.
Persistent Segment Tree를 이용하는 문제로 BOJ 11932 트리와 K번째 수 문제가 있다. 노드의 개수가 N개이고, 각 정점마다 가중치가 있는 트리가 있을 때에 M개의 쿼리에 대해 두 노드 사이를 잇는 경로 상의 K번째 정점 가중치 값을 출력하는 문제이다. 편의를 위해서 가중치들은 다 좌표압축을 하여 1에서부터 N까지의 값만 가진다고 가정하자.
한 쿼리에 대해서 답을 이분탐색하면서 정한 답을 Ans라고 한다면, 두 정점 u와 v 사이를 잇는 경로에 Ans보다 작거나 같은 원소의 개수를 counting해서 그 개수가 K보다 크다면 Ans를 줄이고, K보다 작으면 Ans를 늘이면 된다. 답을 정하는 데에 O(log N)이 필요하고, counting 하는 데에 T만큼의 시간이 걸린다면 쿼리마다 O(T log N)의 시간이 소요된다.
함수 F(p, val)를 트리의 루트 노드부터 p번 노드까지의 경로 상에서 val보다 작거나 같은 원소의 개수를 리턴하는 함수라고 정의하자. 그리고 x를 u와 v의 LCA이고, p(x)를 x의 부모 노드라고 정의하자. 두 정점 u와 v 사이의 경로에서 Ans보다 작거나 같은 원소의 개수 Q(u, v, Ans) = F(u, ans) + F(v, ans) - F(x, ans) - F(p(x), ans)이다.
각 정점마다, root 노드에서 각 노드에 이르는 경로까지의 정점들만을 고려했을 때에 구간 [L, R]에 해당하는 원소 가중치의 값이 몇 개 있는지를 저장하는 Segment tree를 생각해보자. 총 N개의 Segment Tree가 있는 것이다. 그러면 위의 F함수를 계산하는 것을 [1, Ans]까지의 구간합을 구하는 것과 같으므로 O(log N)의 시간이 소요된다. 따라서 T = log N이 되는 것이다. 하지만 메모리 사용량이 각 정점마다 O(N)개의 공간이 필요해서 공간복잡도가 O(N*N)이 된다.
여기서 Persistent Segment Tree가 등장하는데, 어떤 노드 u의 자식 노드 c를 생각해보자. 노드 c에서의 Segment Tree에서는 노드 u에서의 Segment tree에 하나의 원소만이 업데이트 된다. 따라서 총 O(log N)의 구간이 업데이트가 되고 나머지는 다 같다. 따라서 노드 c의 Segment Tree는 노드 u의 Segment Tree를 가리키면서, 새로운 업데이트가 된 구간만 추가해주는 식이다. 그림으로 표현하면 다음과 같다.
각 노드마다 새로운 O(log N)의 구간이 추가되어서 공간복잡도마저 O(N log N)이 되고, Persistent Segment Tree를 구현하는 시간복잡도 또한 공간복잡도에 비례하기 때문에 O(N log N)이 된다. 따라서 전체적으로 시간복잡도는 트리를 구성하는 것과 쿼리에 답하는 것을 합해 O(N log N + M log^2 N)이 된다.
여기서 굳이 답을 결정할 필요가 있을지에 대해 의문을 가져보자. 구간 트리 [L, R]이 왼쪽 부트리 [L, (L+R)/2]와 오른쪽 부트리 [(L+R)/2+1, R]로 나뉜다고 할 때, 트리의 루트에서부터 내려오면서 왼쪽 부트리에 속하는 원소의 개수의 합이 K보다 작다면 우리가 관심있는 K번째 원소는 오른쪽 부트리에 있는 것이고 아니면 왼쪽 부트리에 있는 것이다. 이 Top-Down 방식으로 답을 찾아나가면 트리의 depth는 최대 log N이기 때문에 O(log^2 N)에서 O(log N)으로 시간복잡도를 줄일 수 있다.
따라서 전체적인 시간복잡도는 O(N log N + M log N)이 된다.
'Problem Solving > Data Structure' 카테고리의 다른 글
| C++ [STL] vector 구현 (1) | 2020.08.05 |
|---|---|
| Heavy Light Decomposition (2) | 2018.02.15 |
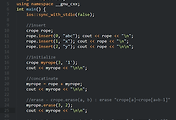
| Rope (0) | 2017.01.19 |
| 트리에서의 Sqrt Decomposition (0) | 2016.05.19 |
| Persistent Segment Tree (0) | 2016.02.25 |



댓글