예전에 kriii가 trello에 남겨주었던 걸 다시 보고 정리하면 좋겠다 싶어서 글을 쓰게 되었다.
프뤼퍼 수열은 정점이 n개인 하나의 labeled tree에 대해 유일하게 결정되는 길이가 n-2인 수열로써, 간단한 방법에 의해 생성된다.
매 step마다 degree가 1인 점들 중 label이 가장 작은 정점을 지우면서 그와 연결된 정점의 번호를 프뤼퍼 수열에 추가한다.
이 수열을 통해 원래의 트리도 복원 가능하므로 트리와 수열이 일대일 대응이 된다.
따라서 labeled tree와 prüfer sequence과의 관계를 통해 n개의 정점을 가지는 서로 다른 labeled tree의 개수는 서로 다른 prüfer sequence의 수와 같으며 개가 된다는 것이 Cayley's formula이다.
이 정리를 응용하면 n개의 정점으로 구성된 완전그래프 에서
번째 정점의 degree를
라 할 때, 가능한 spanning tree의 개수는
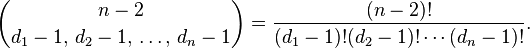
연습문제로는 atcoder New Year Contest 2015 E번이 있다. 예제 설명을 하면 (9-2)! / 2 / 2 = 1260.
'Problem Solving > Algorithm' 카테고리의 다른 글
| Shortest Path Faster Algorithm (0) | 2016.07.28 |
|---|---|
| Divide & Conquer Optimization in DP (3) | 2016.06.12 |
| Lowest Common Ancestor(최소 공통 조상) (0) | 2016.03.31 |
| Smallest Enclosing Circle/Sphere Problem (0) | 2016.02.17 |
| Aho-Corasick Algorithm (0) | 2015.09.27 |

댓글